PRODUIT VECTORIEL

PREPARATION INTERROGATION

( 6 questions traitées en détail )

Exercice 1 : base orthonormale ? directe ou non ? ( 2 questions traitées en détail )

Exercice 2 : équation cartésienne de plan ( 1 question traitée en détail )

 

 Exercice 3 : intersection de plan ( 1 question traitée en détail )

Exercice 4 : aire du triangle ( 2 questions traitées en détail )

 

EXERCICE 1 :

Soit une base orthonormale directe de l’ensemble W des vecteurs de l’espace.

On considère les vecteurs :

1 - Montrer que est une base orthonormale de W.

2 - Cette base est-elle directe ou non ?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

   Solution

1 -

 

 

 

 

 

 

 

 

 

2 - un Théorème de cours donne une direction utile de travail.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

EXERCICE 2 :

L’espace est rapporté à un repère orthonormal direct .

Donner une équation cartésienne du plan P passant par le point  A ( 2, -3, 1 ) et de base où les coordonnées de sont respectivement ( 1, -1, 1 ) et ( 2, 3, 0 ).

 

 

 

 

 

 

 

 Solution

Un plan est caractérisé par un point et un vecteur normal (vecteur non nul et orthogonal à deux vecteurs non colinéaires du plan).

 

 

 

 

 

 

 

 

 

 

EXERCICE 3 :

L’espace est rapporté à un repère orthonormal direct .

On considère les plan P et P’ d’équations respectives

3x - 2y - z + 2 = 0 et x - 2y - z - 3 = 0.

Etudier leur intersection.

 

 

 

 

 

 

 

 

 

 

 

 

   Solution

Les plans P et P’ admettent respectivement pour vecteurs normaux.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

EXERCICE 4 :

L’espace est rapporté à un repère orthonormal direct .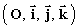

Calculer l’aire du triangle ABC dans les cas suivants :

 

1 - A (2, -1, 1), B (0, -3, 2), C (6, 3, -1).

2 - A (2, -1, 1), B (0, -3, 2), C (2, -3, 4).

 

 

 

 

 

 

 

 

 

 

 

 

 

 Solution

Il s’agit d’une application immédiate de la définition du produit vectoriel.

Pour la détermination du produit vectoriel, on utilise les formules de calcul de ses coordonnées.

1 -

 

 

2 -

 

 

 

 

 

 

 

 

 

 

.