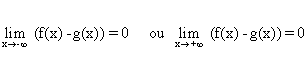LOGARITHME

PREPARATION INTERROGATION

PREPARATION BAC

(12 questions traités en détail)

1 ) Résolution d’une équation avec logarithme( Méthode , 3 questions traitées en détail )

2Ln(2x-1) - Ln (3x-2x²) = ln ( 4x-3) - Lnx

2 ) Résolution d’ inéquations avec logarithme( Méthodes , 3 exercices ,4 questions traitées en détail ) Résoudre:

3 ) Inéquation où l’inconnue est en exposant( Méthodes , 1 question traitée en détail ):

4 ) Etude des variations d’une fonction avec logarithme

sur [0;4] ; f(x) = 2x - (x+1)Ln(x+1)

f (x) = ln(x + 4) + 3. Translation

f(x) = - 2 . Inx. Translation

1 ) Résolution d’ équations avec logarithme : 3 exercices

EXERCICE 1:

On se propose de résoudre dans l’équation .

METHODE:

On cherche l’ensemble des x pour lesquels cette équation existe.

En utilisant les propriétés algébriques de ln, on transforme l’équation pour se ramener à : ln (A) = ln(B).

On applique le théorème "la fonction ln est une bijection" :

ln (A) = ln(B) équivaut à A = B,

et on résout l’équation obtenue.

On vérifie si les valeurs trouvées appartiennent à l’ensemble de définition de l’équation, et on donne l’ensemble solution.

SOLUTION :

Ensemble de définition :

Résolution technique:

Vérification:

REMARQUES PRATIQUES :

Pour chercher l’ensemble solution, il faut se souvenir qu’il y a autant d’inéquations à poser que de ln portant sur des expressions différentes comportant x.

Dans l’écriture de l’équation, si un logarithme est soustrait, il est préférable de le transposer dans l’autre membre.

Par exemple, l’équation ln x - ln (x + 1) = ln 2 devient ln x = ln 2 + ln (x + 1).

Si tous les ln ne portent que sur x (ou la même expression);

par exemple :

Ne pas confondre

De plus, existe pour tout réel, sauf 0.

On ne peut résoudre par un procédé algébrique une équation comme 2 x - 1 + ln (x + 2) = 0, somme d’un polynôme et d’un logarithme de l’inconnue.

Seule une résolution approchée de l’équation f (x) = 0 est possible.

Exercice 2 :

Résoudre dans , l’équation :

METHODE A RETENIR :

- Recherche de l’ensemble de définition D.

- Transformation de l’équation en somme de logarithmes (pour obtenir des produits plutôt que des quotients).

- Utilisation des théorèmes du cors pour obtenir une égalité entre deux logarithmes.

- Utilisation de la propriété ln a = ln b donc a = b pour obtenir une équation sans logarithme.

- Résolution de l’équation - On vérifie que les solutions appartiennent à D.

Solution :

On cherche l’ensemble de définition de cette équation.

L’équation (E) équivaut à :

Exercice 3 :

Résoudre dans R l'équation et l'inéquation suivantes:

2In (x + 1) = In (1 - x) (1)

METHODE :

- Déterminer l'ensemble D de résolution de l'équation (ou de l' inéquation ).

- Se ramener à l'équation In f(x) = In g(x).

- Ne retenir que les solutions qui appartiennent à D.

Solution :

2 ) Résolution d’ inéquations avec logarithme(s) : 4 exercices

EXERCICE 4 :

On se propose de résoudre l’inéquation (un peu compliquée, certes !) :

METHODE

On retrouve les quatre étapes de la méthode de résolution d’une équation et les mêmes remarques techniques.

Seul le théorème à appliquer change.

On utilise alors : "la fonction ln est strictement croissante sur

ln A < ln B équivaut à A < b

Solution :

Ensemble de définition :

Transformons :

L’inéquation devient :

Résolution :

Vérifions :

EXERCICE 5 :

A. Résoudre dans l’inéquation

B. Etudier le signe de l’expression E (x) = ln (1 - x) - 4.

METHODE

A. On retrouve les quatre étapes de la méthode de résolution d’une équation et les mêmes remarques techniques.

Seul le théorème à appliquer change.

On utilise alors : "la fonction ln est strictement croissante sur ".

équivaut à .

Méthode :

B. Pour étudier le signe d’une expression E(x) comportant ln, on résout l’inéquation , c’est-à-dire qu’on cherche pour quelles valeurs de x l’expression est positive ou nulle.

Pour toutes les autres valeurs de l’ensemble de définition, l’expression E(x) sera strictement négative.

Solution :

EXERCICE 6 :

Résoudre dans , l’inéquation :

Solution

On cherche l’ensemble de définition de l’inéquation.

Résoudre :

METHODE :

- Déterminer l'ensemble D de résolution de l'équation (ou de l' inéquation ).

- Se ramener à l'équation In f(x) = In g(x).

- Ne retenir que les solutions qui appartiennent à D.

Solution :

> Mettre l’inéquation donnée sous la forme ln f(x) < ln g(x).

3 ) Inéquation où l’inconnue est en exposant

EXERCICE 8 :

Un capital de 23 000 F est placé à 4,5 % à intérêts composés. Sa valeur acquise au bout de n années est

Déterminer à partir de quelle année sa valeur acquise sera supérieure ou égale à 52 000 F.

METHODE

Pour résoudre une inéquation où l’inconnue est en exposant :

- on utilise la stricte croissance de la fonction ln :

- on divise alors chaque membre de l’inéquation par ln a, en tenant compte de son signe.

SOLUTION :

On cherche n, entier naturel, tel que

4 ) Etude des variations de fonctions avec logarithme (2 exercices )

EXERCICE 9 :

On se propose d’étudier les variations de la fonction numérique de la variable réelle x définie sur l’intervalle

METHODE

- On vérifie que dans l’intervalle donné l’expression f (x) existe, bien que l’ensemble de définition soit donné ici.

- Comme la fonction ln est dérivable sur son ensemble de définition, on calcule la dérivée.

- On étudie le signe de l’expression donnant la dérivée.

- On dresse le tableau des variations sur l’ensemble de définition et on énonce les variations.

SOLUTION :

La quantité dont on prend le logarithme doit être strictement positive.

Courbe :

EXERCICE 10 :

1 ) Etudier la fonction f de R dans R définie par :

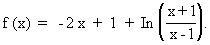
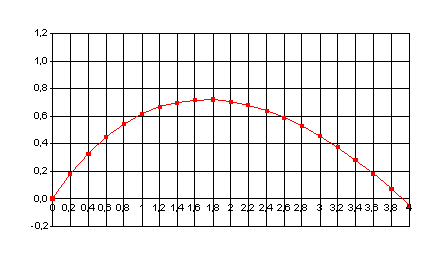
Soit C sa courbe représentative dans un repère orthogonal (O, i, j) ( unités 2 cm sur l'axe des abscisses, 1 cm sur l'axe des ordonnées).

2 ) Démontrer que le point I (0, 1) est centre de symétrie de C et que la droite D d'équation :

y = - 2 x + 1 est asymptote oblique à C.

3 ) Construire C.

METHODES :

1 ) Généralités :

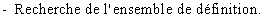
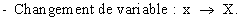
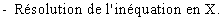
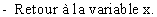
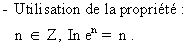
2 ) METHODES A MAITRISER :

- Ensemble de définition fondamental (souvent donné dans l'énoncé).

- Bien connaître les théorèmes sur les limites (opérations, composées).

- Pour montrer qu'une fonction logarithmique est impaire, on utilise la propriété :

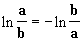
- Pour prouver que la droite A d'équation y = g(x) est asymptote à la courbe C d'équation y = f(x), il suffit de montrer que :

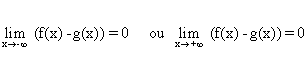
- Ne pas oublier le tableau de valeurs pour construire la courbe précisément.

On se contente de chercher les coordonnées des points situés sur une des deux branches.

On complète en utilisant la symétrie par rapport à I

Solution :

- La fonction f est définie si et seulement si :

Graphe :

Exercice 11 :

Etudier et représenter la fonction f définie sur ]- 4 ; +00 [ par :

f (x) = ln(x + 4) + 3.

Méthode :

Si la fonction f est telle que f (x) = In (x - a) + b, alors la courbe de la fonction f est la transformée de la courbe F d'équation y = In x

dans la translation de vecteur V(a; b).

La fonction f a même sens de variation que In.

Solution :

D'où le tableau complet des variations :

Graphe :

Exercice 12 :

Etudier et représenter la fonction f définie sur ]- 4 ; +00 [ par :

f(x) = - 2 . Inx.

MÉTHODES :

Si la fonction f est telle que f (x) = k . In x, alors en multipliant par k l'ordonnée de chaque point N( x ; ln x) de z d' d'équation y = In x, on obtient les points M(x; k.ln x) de la courbe C_f .

Solution :

D'où le tableau complet des variations :