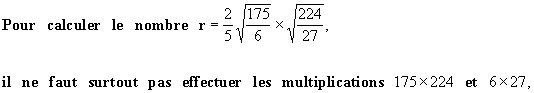I - L’ESSENTIEL DU COURS A MAITRISER
PARFAITEMENT
II - METHODES DE
RESOLUTION ET PREPARATION INTERROGATION :
L’ESSENTIEL DU COURS A MAITRISER
PARFAITEMENT
:
| Pour tout nombre positif a le nombre positif x
tel que x² = a
est appelé la racine carrée de a et se note 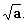
|
| Dans toutes les égalités suivantes, a, b et x sont des nombres
positifs. 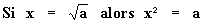
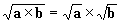
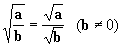
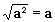
Ne pas oublier que:
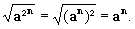
Exemple:
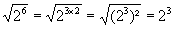
a et b n’étant pas nul, on a toujours:
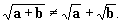
Quand on hésite dans un exercice, prenez un exemple:

|
Exemple 1 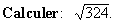
Solution:
Exemple 2
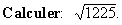
Solution:
|
Méthode 1 :
| Pour calculer avec des racines carrées, il est utile de savoir
transformer des expressions contenant des radicaux.
Présentation des situations les plus fréquentes.
Réduire des sommes : |
Exercices 1 à 9 :
| Exercices 1 et 2 On donne
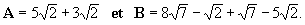
Réduire les expressions A et B.
|
Solution :
|
Exercices 3 à 9 :Trouver les racines carrées suivantes
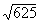 |
Solution :
|
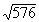 |
Solution :
|
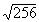 |
Solution :
|
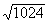 |
Solution :
|
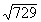 |
Solution :
|
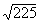 |
Solution :
|
METHODE 2

| METHODE : A/ On transforme c en un produit de
facteurs.
B/ On extrait les racines carrées simples qui apparaissent.
C/ On multiplie ces derniers nombres entre eux. l
es autres restent sous le signe 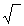 et
se multiplient sous ce signe. et
se multiplient sous ce signe.
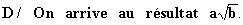
|
Exemple 1: 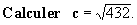
Solution:
Exemple 2 :
|
EXERCICES 10 à 16 :
Ecrire les racines carrées suivantes sous la forme 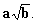
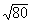 |
Solution: |
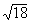 |
Solution: |
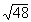 |
Solution: |
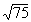 |
Solution: |
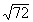 |
Solution: |
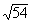 |
Solution: |
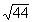 |
Solution: |
Méthode 3 :
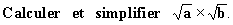
| METHODE : A/ On cherche à remplacer a et b par
un produit de facteurs.
B/ On calcule les racines carrées qui apparaissent et on les multiplie entre
elles.
C/ On multiplie éventuellement entre elles les racines irréductibles
provenant de a et b.
D/ On arrive au résultat de forme générale 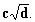
|
Exemple 1 : En appliquant ces mêmes
règles, il est possible de simplifier l’écriture du nombre m :
Exemple 2 :
|
Pour calculer 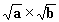 , il
n''est pas opportun de commencer par effectuer la multiplication
, il
n''est pas opportun de commencer par effectuer la multiplication 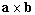 , ainsi, dans les exemples précédent, calculer 80X125 ou 72X108 serait du
temps perdu et une source d’erreurs.
, ainsi, dans les exemples précédent, calculer 80X125 ou 72X108 serait du
temps perdu et une source d’erreurs.
EXERCICE 17 à 21 :
Calculer et simplifier:
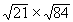 |
Solution: |
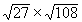 |
Solution: |
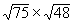 |
Solution: |
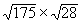 |
Solution: |
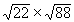 |
Solution: |
METHODE 4 :
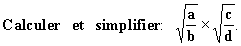
| On applique les méthodes précédente pour procéder à la
décomposition en produits de facteurs des numérateurs et des dénominateurs avant de
multiplier les racines entre elles.
On extrait ensuite les racines carrées simples qui apparaissent.
|
Exemple: 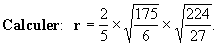
Solution:
|
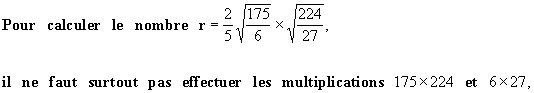
Mais d’abord décomposer ces nombres en facteurs, puis,
simplifier.
EXERCICE 22 à 25 :
Calculer et simplifier:
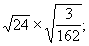 |
Solution : |
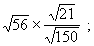 |
Solution : |
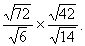 |
Solution : |
Méthode :
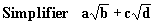
| Exemple: 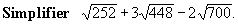
|
Solution:
|
EXERCICES 26 à 29 :
Simplifier:
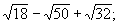 |
Solution: |
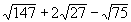 |
Solution: |
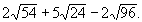 |
Solution: |
méthode :