CH 10
STATISTIQUES
PREPARATION INTERROGATION
1 - DIAGRAMME EN BATONS :
| EXERCICE :
Répartition par branches
d’activite d'un groupe industriel :
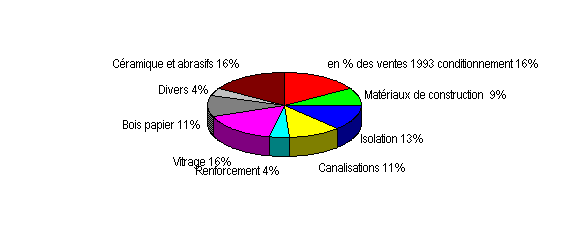
1 ) Répartition par branches
Représentez la répartition par branches de
l'activité du groupe
à l'aide d'un diagramme en bâtons.
METHODES :
Dans un diagramme en bâtons, les hauteurs des
bâtons sont
proportionnelles aux
pourcentages.
|
| SOLUTION :
Pour 0,5 cm pour 2 % en ordonnée.

IL S'AGIT D'UN DIAGRAMME EN BATON EN 3 D
|
2 - DIAGRAMME CIRCULAIRE
| EXERCICE : Répartition
des ventes par marque en 1993

Ce diagramme donne la répartition par marque des ventes de 4 x 4 en
France.
Construisez un diagramme circulaire donnant cette répartition.
METHODE :
Dans un diagramme circulaire, l'angle au centre
de chaque secteur
est proportionnel au pourcentage. Faites un
tableau de
proportionnalité pour le coefficient de
proportionnalité.
est (360° pour 100 %). |
| SOLUTION :

|
3 - HISTOGRAMME
| Exercice : Au 1er janvier 1994,
26,4 % des habitants de la France ont moins de 2 ans,
58,9 % ont entre 20 et 64 ans et
14,7 % ont 65 ans et plus
(I.N.S.E.E., T.E.F, 93/94).
Construisez un histogramme donnant la répartition de la population française
suivant l'âge au 1/1/1994.
METHODE :
L'aire de chaque rectangle doit être
proportionnelle au pourcentage.
Vous connaissez la largeur du rectangle (c'est
la longueur de
l'intervalle).
Construisez un tableau pour en déterminer la
hauteur.
|
SOLUTION :
Choisissons 100 ans comme borne supérieure du dernier intervalle.
Les trois intervalles sont alors [0, 20 [ ,
[20, 65[ et [65, 100].
(Explications : 
Répartition de la population française par classe d'âge :
Unité: 1 cm pour 20 ans

|
4 -
MOYENNE. ECART TYPE
| EXERCICE : Le
tableau ci-après donne la distribution des
salaires annuels nets de prélèvement des agents titulaires de la
fonction publique en 1992.
1° Déterminez la moyenne 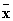 et l'écart type et l'écart type 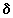 de cette série statistique. de cette série statistique.
2° Déterminez le pourcentage des personnes dont le salaire appartient
à l'intervalle
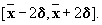

METHODE :
Pour les calculs, on prend le milieu de la
classe. La première et la
dernière classe doivent être arbitrairement
bornées.
Pour calculer l'écart type, on a le choix
entre deux formules
Lorsque les valeurs des xI sont grandes (comme
c'est le cas ici), la
première formule est la plus indiquée.
|
SOLUTION :
1° On suppose que la première classe est [70000, 74810] et la
dernière
[226820, 270000].
Calcul de 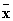 (xi
est le milieu de la classe) (xi
est le milieu de la classe)

Calcul de 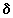

Donc : 
et 
2° 

Près de 95 % de l'effectif a un salaire appartenant à l'intervalle |
5 - INDICES
| EXERCICE : 1°
Production
Reprise confirmée, mais fragile, dans l'industrie
Indice CVS, base 100 en 1985
113,6 113,6
113,10 110,90 109,10
108,5 109,1
107,90 108,6
1T/92 2T/92
3T/92 4T/92
1T/93 2T/93
3T/93 4T/93
1T/94
lnfomatin. 10/8/94
a) Déterminez les nouveaux indices de la production industrielle en
choisissant, pour base 100, le 1er trimestre 92.
b) Déduisez-en la variation en pourcentage de la production
industrielle de la
France entre le 1er trimestre 92 et le 1er trimestre 93; entre le 1er
trimestre 92
et le 1er trimestre 94.
2° Dette de l'état
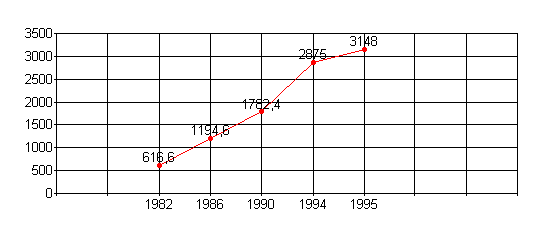
a) En choisissant pour base 100 l'année 1992, déterminez l'évolution
de la
dette de l'état français.
b) Quelle est l'augmentation en pourcentage entre 1982 et 1986 ? Entre
1982
et 1995?
COMMENTAIRE :
Les indices permettant d'évaluer une
évolution en pourcentage par
rapport à une année de référence. Il suffit
de remplir un tableau de
proportionnalité, le coefficient étant pour
la question 1°

et pour la question
2°.
 |
SOLUTION
1° a)
b) La production industrielle a baissé de 4 % entre le 1er,
trimestre 92 et le 1er
trimestre 93; et de 4,4 % entre le 1er trimestre 92 et le 1er trimestre
94.-
2° a)

b)
Entre 1982 et 1986, la dette augmente de 93,7 %.
Entre 1982 et 1995, la dette augmente de 410,5 %.
|
6 - PROPORTIONS :
EXERCICE :
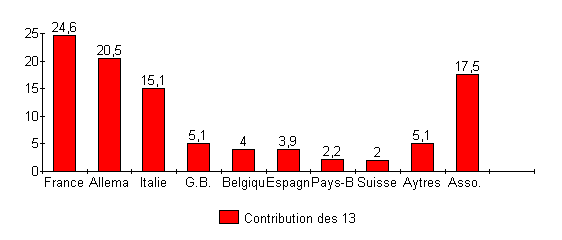
Le dessin ci-dessus donne, en pourcentages, les contributions des
différents
pays membres de l'ESA (Agence spatiale Européenne).
La contribution de la France au projet Hermès construction d'une
navette
spatiale européenne est d'environ 12,5 milliards de francs (MdF).
A partir de ces données, évaluez en milliards de-francs :
a) Le budget global du projet.
b) La contribution de chacun des membres de l'ESA, au projet.
METHODE :
L'ensemble de référence étant le même
(budget global du projet), les
contributions de chaque membre, en francs, sont
proportionnelles
aux pourcentages indiqués sur le diagramme.
|
SOLUTION :
Désignons par B le budget global du projet.
a) En ce qui concerne la France, on a la
proportion : 
b) La contribution de l'Allemagne,
notée a, s'obtient en écrivant la proportion :

Les autres résultats s'obtiennent de la même manière. Le
tableau suivant résume l'ensemble de ces résultats :

|
7 - ENSEMBLES ET POURCENTAGES
| EXERCICE : Dans un
magasin, un stock d'appareils est constitué pour 70 % d'appareils venant d'une usine A et
pour 30 % d'appareils venant d'une usine B.
Parmi les appareils venant de A, 15 % ont un défaut, alors que 10 % de
ceux venant de B ont un défaut.
1° Quel est, dans le stock, le pourcentage d'appareils ayant un
défaut ?
2° Parmi les appareils ayant un défaut, quel est le pourcentage de
ceux provenant de A?
3° Parmi les appareils n'ayant pas de défaut, quel est le pourcentage
de ceux provenant de B ?
METHODE :
Les données de l'énoncé, sous la forme de
pourcentages, sur des ensembles de référence variés. Pour mieux représenter la
situation, il est souhaitable d'utiliser un diagramme pour mettre en évidence les
données.
|
SOLUTION Désignons
respectivement par S, A, B, D,  les ensembles des
appareils du stock, des appareils fabriqués par A, de ceux fabriqués par B, de ceux qui
sont défectueux et enfin des appareils sans défaut. les ensembles des
appareils du stock, des appareils fabriqués par A, de ceux fabriqués par B, de ceux qui
sont défectueux et enfin des appareils sans défaut.
-  est l'ensemble des appareils
défectueux, provenant de A et est l'ensemble des appareils
défectueux, provenant de A et

est l'ensemble de ceux défectueux provenant de B.

-  est l'ensemble des appareils sans
défaut provenant de A et est l'ensemble des appareils sans
défaut provenant de A et  .l'ensemble de ceux, sans défaut, provenant de B. .l'ensemble de ceux, sans défaut, provenant de B.
1° Désignons par n l'effectif du stock.
On en déduit que :
- L'effectif de A est  et celui de B est et celui de B est  . .
- L'effectif des appareils défectueux provenant de A est 
et celui de ceux provenant de B est 
Globalement :  appareils sont
défectueux. appareils sont
défectueux.
Le pourcentage des appareils défectueux est donc le nombre

Remarque : Vous constatez que la valeur de n
n'intervient pas dans le pourcentage, ce qui justifie le fait qu'il n'était pas précisé
dans l'énoncé.
2° Dans cette question L'ensemble des référence est
l'ensemble D. Le pourcentage, parmi les appareils défectueux, de ceux provenant de A est
le nombre :
 
Soit 77,78 %.
3° L'ensemble de référence est l'ensemble des appareils sans
défaut.
Le nombre de ces appareils est égal à
n - 0, 135n = 0,865n et parmi ceux-ci
0,3n - 0,03n = 0,27
0n proviennent de B.
Le pourcentage des appareils sans défaut, provenant de B, est le
nombre :
 |
8 - ARBRE ET
POURCENTAGE
| EXERCICE : On
considère les participations en capital suivantes.

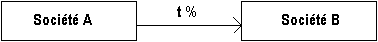
signifie que la société A possède t % du capital de la
société B. La part de la
société A, dans les avoirs de la société B est donc, en
pourcentage,
égale à t %.
1° a) Quelle est la part, en pourcentage, détenue par la société
U.A.P., à
travers la Compagnie
Industrielle exclusivement, dans le capital du
groupe Victoire ?
b) Déduisez-en la part de l'U.A.P. dans le capital du groupe Victoire,
part
obtenue directement et part indirecte obtenue
à travers la Compagnie
Industrielle.
2° a) L'U.A.P. possède aussi, au travers de la compagnie Suez, une
part du
capital de Victoire. Calculez cette part.
b) Faites le bilan final de la participation, en pourcentage, de
l'U.A.P.
dans le capital de Victoire.
3° a) Déduisez-en la part, en pourcentage, de l'U.A.P. dans le
capital de
Colonia Konzern.
b) Refaites les calculs pour déterminer dans ce même capital la part
en
pourcentage, de la compagnie Suez.
METHODE :
Cet exercice porte essentiellement sur la
notion de pourcentages
|
SOLUTION :
Les réponses aux diverses questions s'obtiennent en utilisant la
règle des
pourcentages de pourcentages (les pourcentages sont alors écrits sous
leur
forme décimale).
1° a) La part de l'U.A.P., à travers la Compagnie
Industrielle, est égale à :
0,501 x 0,461 = 0,231 du capital du groupe
Victoire, soit 23,1 % de
celui-ci.
b) L'U.A.P. possède donc indirectement 23,1 %
auxquels s'ajoutent 10,9 %
de part directe soit, au total, 23,1 + 10,9 =
34 % du capital du groupe
Victoire.
2° a) A travers Suez et la Compagnie industrielle, l'U.A.P. possède
aussi une
part du capital du groupe Victoire. Celle-ci
est égale à :
soit 3,1 % de ce
capital.
b) Finalement, l'U.A.P. possède 34 % + 3,1 % =
37,1 % du capital du
groupe Victoire.
3°
a) Le groupe Victoire contrôle 78,8 % du
capital de Vinci qui contrôle
lui-même 75 % du capital de Colonia Konzern.
L'application de la règle des pourcentages de
pourcentages indique
que l'U.A.P. possède :
0,371 x 0,788 x 0,75 =
0,219 du capital de Colonia Konzern,
soit 21,9 % de
celui-ci.
b) La compagnie Suez possède 0,501 x 0,501 +
0,271, soit 0,522 du
capital du groupe Victoire, soit 52,2 % .Sa
part du capital de Colonia
Konzern est donc égale à :
0,522 x 0,788 x 0,750 =
0,309 de celui-ci soit 30,9 %. |
9 - POURCENTAGE ET ARTICLE ECONOMIQUE
| EXERCICE : Avec une croissance limitée à
moins de 1% au mois d'août, la stagnation du marché automobile français se confirme.
Depuis le début de l'année, la progression des ventes reste cantonnée à un modeste
0,17%. Sur les 152364 véhicules commercialisés le mois dernier, Renault s'est taillé
là part du lion. En hausse de 20 % par rapport au mois d'aoùt 1991, les ventes de la
Régie, grâce à la Clio et à la R19 notamment, ont
représenté 31,4% du marché. Par contraste, celles du groupe PSA, en baisse sensible, ne
dépassent pas 28,1% de part de marché en dépit des résultats honorables de Citroën.
1° a) Quel est le nombre de voitures commercialisées par Renault en août 1992 ?
b) Déduisez-en le nombre de voitures commercialisées par Renault en
aoû 1991.
2° Quel est le nombre de voitures vendues par
le groupe PSA* en août 1992 ?
3° Dire que le marché automobile a augmenté
de 1% en août 1992 signifie que les ventes d'août 1992 sont supérieures de 1 % à
celles d'août 1991.
a) Combien de voitures
ont été vendues en France en août 1991 ?
b) Déduisez-en la
part, en pourcentage, de Renault en août 1991.
METHODE :
Dans cet exercice, bâti à partir d'un article de journal, vous êtes invités à
compléter certaines informations, soit en données absolues, soit en données
relatives (pourcentages).
Les solutions seront obtenues à partir de la définition d'un pourcentage
d'évolution.
|
SOLUTION : 1°
a) y désigne le nombre de voitures vendues par Renault en 1992; alors :

b) Si nous désignons par x les ventes de Renault en août
1991, l'augmentation de 20% se traduit par :

Vous avez vu, en cours, qu'une augmentation de t % (ici t = 20)
d'une grandeur x se traduit par une multiplication de x par

soit ici par 1,20.
En utilisant cette remarque on pouvait donc écrire : 
2° La part de PSA est de 28,1% dans un marché de 152 368 véhicules soit
environ 42 814 unités.
3° a) Le marché ayant augmenté de 1% d'août 1991 a août 1992, le
nombre de véhicules vendus, en France, en août 1991 était donc

soit environ 150855.
b) La part de Renault dans ce marché d'août 1991 était donc, en
pourcentage :

|
10 - REGROUPEMENTS
EN CLASSES. HISTOGRAMMES
| EXERCICE : HISTOGRAMMES

Un correcteur communique la répartition des notes obtenues par 50
candidats
en donnant le diagramme en bâtons ci-dessus.
Il propose aussi trois regroupements en classes :
1° Des classes d'égale amplitude :
[0,5[, [5, 10[, [10, 15[, [15,20[;
2° Des classes à bornes fixées :
[0, 8 [, [8, 10 [, [10, 12 [, [12, 14 [, [14,
16 [16, 20[.
3° Des classes à effectif égal : 10.
Après avoir opéré chaque regroupement, vous construirez
l'histogramme
correspondant, vous repérerez le mode ou la classe modale, et vous
déterminerez avec votre calculatrice la moyenne et l'écart type.
Quels sont les avantages et les inconvénients des divers regroupements
?
METHODE :
- L'un des intérêts
d'un tableau, par rapport à une liste, dans la
présentation des
données est de faciliter la lecture.
- Il y a ainsi
nécessité pour la personne qui reçoit l'information de
bien lire le tableau :
par exemple, 4 élèves ont obtenu la note 3 et
5 élèves la note 9.
- Pour calculer
l'effectif de la classe [0,5[, on ajoute le nombre
d'élèves ayant obtenu
la note 0 successivement aux nombres
d'élèves ayant obtenu
la note 1, la note 2, la note 3 et la note 4.
|
| SOLUTION :
1°

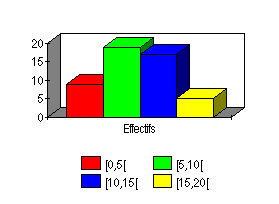
La classe modale est la classe ayant le plus grand effectif. Il s'agit
donc de la
classe [5,10[.
La moyenne est :

L'écart type est : 
2°
 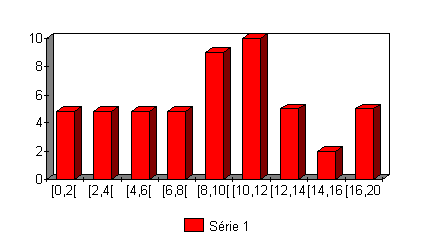
La classe modale est : [8,0[. La moyenne est : 9,04.
L'écart-type est : 4,63.
3° Pour opérer le regroupement en classes à effectif égal, on utilise le
polygone des effectifs cumulés croissants.

On déduit de ce diagramme le regroupement même fréquence 20%) :

Dans cet histogramme, tous les rectangles ont la même aire.
La classe [0, 5] a pour effectif 10 élèves : il y a 9 élèves qui
ont obtenu 4 ou
moins de 4, le 10e a obtenu 5.
Dans la classe [5, 8], on compte du 11e élève qui a obtenu 5 au 20e
élève qui
a obtenu 8, et ainsi de suite...
La moyenne est :

L'écart type est : 4,5.
|
11 - CALCUL DE LA
MEDIANE PAR INTERPOLATION LINEAIRE
| EXERCICE : Le
tableau suivant donne le nombre des entreprises de l'agro-alimentaire en fonction de
l'effectif des salariés en 1985.

(Source I.N.S.E.E.)
Calculez la médiane de cette série statistique.
METHODE :
Dans cet exercice, la médiane est le nombre m de salariés pour lequel
la
moitié des entreprises (soit 50 % des entreprises) a un effectif
inférieur
ou égal à m, et l'autre moitié un effectif supérieur ou égal à m.
|
SOLUTION :
Nous complétons ce tableau par celui des fréquences cumulées.
Nous constatons que 67,3% des entreprises ont un effectif inférieur ou
égal à
49 salariés. Comme 26% des entreprises ont un effectif inférieur à
20 salariés,
la médiane appartient à la classe [20, 49].
on utilisera l'intervalle [20, 50 [.
Déterminons la valeur de la médiane à l'aide du nombre
d'entreprises.
L'effectif moitié est de 3 898 : 2 = 1 949.
On détermine les effectifs cumulés successifs jusqu'à celui qui
dépasse
l'effectif moitié.
Dans la deuxième classe, on a : 1 610 + 1 014 = 2 624.
On effectue ensuite une interpolation linéaire dans la classe [20, 50
[.
Cela signifie
que, par approximation, on suppose les effectifs salariés également répartis à
l'intérieur de cette classe.

L'effectif de 1 610 salariés correspond à une différence de 30 sur
l'axe des
abscisses.
L'effectif de 1 949 - 1 014 = 935 correspond donc à une différence de
:

La médiane est alors : 20 + 17 = 37.
Remarque :
Le raisonnement ci-dessus, appelé interpolation linéaire,
utilise l'équation de la droite (AB) de la figure, et la
recherche de l'abscisse d'un point M de cette droite
connaissant son ordonnée.
|
12 - PYRAMIDES DE SALAIRES ( HOMMES FEMMES )
EXERCICE :
On donne les pyramides des salaires pour les hommes et les femmes du
secteur privé et semi-public, en 1984 et 1991.
Salaires mensuels nets par tranche de 10 % en francs 1991
HOMMES

1984 1991
FEMMES

1° Donnez le salaire médian chez les hommes et chez les femmes, en
1984 et
en 1991.
Quel est le pourcentage d'augmentation du salaire médian entre 1984 et
1991 chez les hommes ? chez les femmes ?
2° Calculez le rapport entre le salaire du dixième le mieux
rémunéré et le
salaire du dixième le moins rémunéré chez les hommes en 1984, puis
en
1991.
3° Effectuez le même calcul chez les femmes.
4° Quelle conjecture pouvez-vous tirer concernant l'éventail des
salaires
féminins et masculins ?
METHODE :
Le tableau concerne les personnes qui
travaillent dans le secteur
privé et semi-public.
L'étendue des salaires n'est pas donnée ; le
pourcentage d'hommes
et de femmes dans cette population n'est pas
donné non plus.
Le salaire médian est le salaire tel que la
moitié des salariés gagne
davantage et la moitié gagne moins.
|
SOLUTION
1° Le salaire médian chez les femmes était de 6 510 F par mois en
1984 ;
sept ans après il est de 7 010F.
Or 
Le salaire médian chez les femmes a donc progressé
d'environ 7,7%.
Le pourcentage d'augmentation chez les hommes durant
cette période n'est
que de 4,8%.
2° Chez les hommes en 1991 on calcule le rapport 
Chez les hommes en 1991 on calcule
le rapport On trouve
environ 3,2. En 1984, ce rapport était de 3,1.
.
3° En 1991, chez les femmes, ce rapport est de
2,5. En 1984, il était de 2,4.
4° On peut dire que l'éventail des salaires
féminins est moins ouvert que
celui des hommes ; c'est-à-dire que lorsque
les femmes montent dans la
hiérarchie, elles sont moins bien payées que
les hommes qui montent ou
bien elles n'accèdent pas aux postes les mieux
rémunérés.
|
13 - EFFECTIFS, FREQUENCE, MARGINAUX.
| EXERCICE : Les résultats de l'étude de deux
caractères X et Y sur une certaine population
sont présentés dans le tableau d'effectifs suivant :
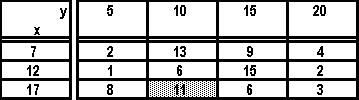
1° Calculez
1° Calculez les effectifs marginaux. Quel est
l'effectfif total ?
2° Déterminez les fréquences marginales
suivant le caractère X, puis
suivant le caractère
Y.
3° Quel est le pourcentage d'individus parmi
la population totale possédant
la valeur 15 du caractère Y ?
4° Quel est le pourcentage d'individus parmi
la population totale possédant
la valeur 12 du caractère X ?
METHODE :
- La population étudiée n'est pas précisée.
- Il s'agit d'un tableau d'effectifs.
L'importance numérique de cette
population est donc la somme des effectifs
contenus dans toutes
les cases du tableau.
- Le caractère X prend les valeurs 7, 12 et
17.
La caractère Y prend les valeurs 5, 10, 15 et
20.
- Le tableau comporte 3 lignes et 4 colonnes.
- Le nombre N32, égal à 11, signifie qu'il y
a 11 individus associés au
couple (17, 10), c'est-à-dire possédant à la
fois la valeur 17 du
caractère X et la valeur 10 du caractère Y.
- Les marges ne sont pas données ; c'est
l'objet de la question 1° . |
SOLUTION
On vérifie ce résultat en effectuant la somme des
effectifs de la ligne "total".

1° On obtient les effectifs marginaux en
additionnant les effectifs par ligne et
par colonne.
La somme des effectifs de la colonne “total” donne l'effectif
total.
On vérifie ce résultat en effectuant la somme des effectifs de la
ligne “total”.
L'effectif total est de 80 individus.
2° Les fréquences marginales suivant le
caractère X se placent en marge
de la colonne “total”.
On calcule les pourcentages correspondant aux effectifs marginaux :
par exemple, pour la valeur 7 du caractère X, l'effectif est de 28,
l'effectif
global étant de 80, la fréquence marginale x (exprimée en %)
correspondante
est donnée par :
Les fréquences marginales suivant le caractère Y se placent en
marge de la
ligne “total”.
On calcule les pourcentages correspondant aux effectifs marginaux.
3° Le pourcentage d'individus possédant la
valeur 15 du caractère Y se lit
dans la ligne “fréquences
marginales”. Il est de 37,5%.
4° Le pourcentage d'individus possédant la
valeur 12 du caractère X se lit
dans la colonne “fréquences marginales
”. il est de 30%.
|
14 - REPARTITION DE POPULATION SUIVANT DEUX CARACTERES
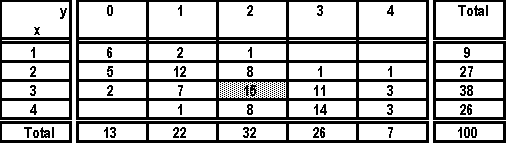
| EXERCICE : Le
tableau suivant donne la répartition d'une population de 100 ménages selon les deux
caractères X et Y suivants . X, nombre de pièces habitées et Y, nombre
d'enfants.
1° Dressez le tableau des fréquences par rapport aux nombres d'enfants pour
chaque type de logement.
2° Dressez le tableau des fréquences par rapport aux types de logement pour
chaque catégorie de ménages.
3° Répondez aux deux questions suivantes :
a) Parmi les familles ayant 2 enfants, quel est le pourcentage de celles
habitant 3 pièces ?
b) Parmi les familles habitant 3 pièces, quel est le pourcentage de celles qui
ont 2 enfants ?
4° Construisez le tableau théorique obtenu par produit des fréquences
marginales et comparez avec le tableau donné en construisant le tableau des écarts.
Tableau des fréquences - tableau théorique - tableau des écarts
METHODE :
- La population étudiée est de 100 ménages. Le tableau d'effectifs donné
peut donc aussi s'interpréter comme un tableau des fréquences.
- Les marges représentent alors à la fois la répartition marginale et les
fréquences marginales exprimées en %. |
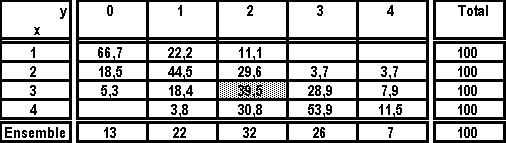
| SOLUTION : 1° Le
tableau des fréquences par rapport aux totaux de lignes donné, pour chaque nombre de
pièces, la répartition des familles selon le nombre d'enfants.
Par exemple pour la valeur (3, 2) du couple (X, Y), l'effectif est de 15
; l'effectif total de la 3 e ligne étant de 38, la fréquence f (exprimée en %) par rapport au total de
la ligne pour cette valeur (3, 2) est donnée par :

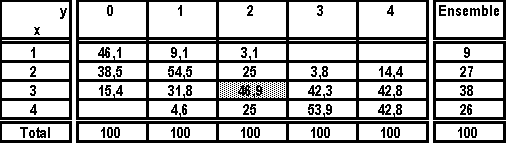
2°
Le tableau des fréquences par rapport aux totaux de colonnes
permet d'avoir, pour chaque nombre d'enfants, la répartition des familles selon le nombre
de pièces.
3°
a) 46,9 % b) 39,5%
4° Le tableau théorique se construit en faisant le produit des
fréquences marginales.
Par exemple :  que l'on arrondit
à 1%. que l'on arrondit
à 1%.
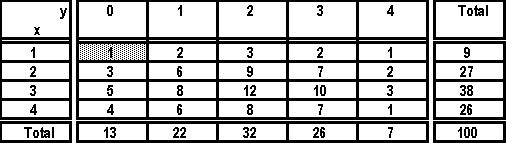
Par différence entre les deux tableaux, on obtient le tableau
des écarts :
 |
|