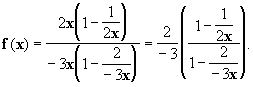| LIMITES
ASYMPTOTES
32 questions traitées
PREPARATION INTERROGATION
L
1 -
LIMITES EN a
| METHODE :
Rappelons que si une fonction est définie en a, alors sa limite en a est
égale à f(a).
C’est le cas pour les deux premiers calculs.
Les deux calculs suivants nécessitent une simplification du quotient.
Les deux dernières limites sont indéfinies.
On doit déterminer le signe du dénominateur pour les trouver.
|
Calculez les limites suivantes : ( 6 questions
traitées)
a) lim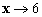  
|
SOLUTION a)
|
|
SOLUTION b)
|
|
SOLUTION c)
|
|
SOLUTION d)
|
 
|
SOLUTION e)
|
 
|
SOLUTION f)
|
2 -
LIMITES EN L’INFINI ( 6 questions
traitées)
| METHODE
:
Utilisez les propriétés concernant les opérations et les limites.
Dans les cas d’indétermination, vous pouvez factorisez le polynôme par
le terme de plus haut degré (b) ou, dans les cas de quotient, factorisez le numérateur
et le dénominateur par le terme de plus haut degré (e et f). |
Calculez les limites suivantes :
| a) 
|
SOLUTION : a)
|
| b) 
|
SOLUTION : b)
|
c) lim   |
SOLUTION : c)
|
d) lim 
|
SOLUTION : d)
|
e) lim  
|
SOLUTION : e)
Donc
|
f) lim 
|
SOLUTION : f)
On peut écrire, pour tout x>0 :
Or
Donc
|
3 - FONCTION HOMOGRAPHIQUE ( 7 questions
traitées )
| Exercice : Soit f :
On appelle (C) la courbe représentative de f dans un repère
orthonormal 
1° Déterminez les nombres réels a et b tels que, pour tout x éléments de
 , on a : 
2) Déterminez le signe de 2x + 6 sur  .
3) Calculez la limite de f en - 3.
4) Montrez que (C) admet une asymptote verticale dont vous donnerez une
équation.
5) Calculez la limite de f en 
6) Montrez que (C) admet une asymptote horizontale. Précisez une équation de
cette droite.
7) Tracez (C) et ses deux asymptotes.
METHODE :
La fonction f est homographique. C’est à dire
qu’elle est la quotient de deux polynômes de degré 1.
La courbe représentative d’une telle fonction admet toujours deux
asymptotes.
Une asymptote verticale d’équation 
où  est la valeur annulant le dénominateur (ici ).
Une asymptote horizontale d’équation y = a, où a est le nombre
déterminé dans la question 1°.
Pour déterminer a et b, réduisez  au même
dénominateur, puis identifiez le numérateur à 3x-1. au même
dénominateur, puis identifiez le numérateur à 3x-1. |
SOLUTION 1° Pour
tout x élément de :
Identifions 2ax + (6a + b) = 3x - 1. On obtient :
2)
3)
Donc
Or
4)
5)
6)
|
7) Graphe
4 - ASYMPTOTES PARALLELES AUX AXES ( 3
questions traitées )
| Exercice : Soit
f la fonction définie sur 
par :
1) Déterminez les limites de f en  et en 0.
2) Déterminez les limites de f en 0.
3) Interprétez graphiquement ces résultats.
METHODE :
- La fonction f est défini sur  .
Lorsque vous chercher la limite de f en o, n’oubliez pas que x est
strictement négatif.
- L’interprétation graphique des résultats est une application directe
du cours
|
SOLUTION :
D’où
|
5 -
ASYMPTOTE VERTICALE ( 4 questions traitées
)
| Exercices : 1° Soit f la fonction
définie sur [1,5] par :
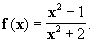
a) Montrez que f s’annule en 1.
b)
Déterminez le signe de f(x) sur l’intervalle
] 1 , 5 ].
2°) Soit g la fonction définie sur ]1,5] par :
a) On note (C) la courbe représentative de g dans un repère orthogonal  .
Montrez que la droite (D) d’équation x = 1 est une asymptote à (C).
b) Construisez (C) et la droite (D).
METHODE :
- La première question sert à montrer que la fonction g admet une limite
infinie en 1.
Le signe de f(x) sur l’intervalle ] 1 , 5 [ permet de préciser si la
limite est  ou .
- Pour déterminer ce signe, on va factoriser le numérateur et construire un
tableau de signes.
- La fonction g est définie sur ]1,5] et a une limite infinie en 1. Choisissez
les unités en conséquence et placez judicieusement le repère.
Si on dispose d’une calculatrice graphique, on fait quelques essais en
modifiant les données dans la fonction "RANGE".
|
SOLUTION : 1° a)
b)
D’où le tableau de signes :
2°
a)
La courbe représentative de g admet donc la droite d’équation x=1 pour
asymptote verticale.
|
ES
6 ASYMPTOTE OBLIQUE ( 3
questions traitées )
| EXERCICE : On considère la fonction f
définie sur 
par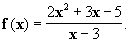 
On appelle (C) la courbe représentative de f dans un repère orthogonal  .
1° Déterminez les nombres réels a, b et c tels que, pour tout x élément de
,
on a
2° Montrez que la droite (D) d’équation y = 2x + 3 est une asymptote à
(C) en .
3° Tracez (C) et (D) dans le repère  .
METHODE:
- Après avoir réduit 
au même dénominateur, il suffit d’identifier le numérateur à celui de
f(x).
- La nouvelle écriture de f(x) permet d’après la question 2° de dire
que a = 2 et b =3. |
SOLUTION : 1° Pour tout x élément de 
,
On identifie
Conclusion :
2°
|
S
7 LIMITE D’UNE FONCTION
RATIONNELLE EN , en ( 2 questions traitées )
| Exercice : f est la fonction rationnelle
définie sur son domaine de définition par
1 ) Etudiez la limite de f en .
2) Etudiez la limite de f en .
METHODE :
Pour étudier la limite en , ou
en , d’une fonction rationnelle
 ,
en général, on met en facteur le monôme de plus haut degré dans P(x) et le
monôme de plus haut degré dans Q(x).
|
SOLUTION :
Après avoir mis 2x en facteur au numérateur et - 3x en
facteur au dénominateur, on obtient :
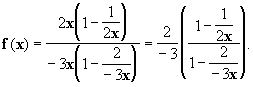
On voit de même que
REMARQUE :
|
8
ETUDIER LA LIMITE D’UN QUOTIENT 
EN UN POINT a TEL QUE (a) = 0 ET N(a)  0
| EXERCICE : f est la fonction définie
sur  par
Etudiez la limite de f en 1.
METHODE :
Pour étudier la limite d’un quotient  en un point a tel que D(a) = 0
et N(a) 0,
- on cheche la limite de N au point a ;
- on étudie le signe de D "autour du point a" ;
- on utilise le théorème sur la limite d’un quotient, en distinguant, si
ce signe n’est pas constant "autour de a", limite à droite et limite à
gauche.
|
SOLUTION : On sait que
On détermine alors le signe de (x-1) :
Donc,
On voit de même que :
|
|
EN UN POINT a TEL D(a) = 0 ET N(a)