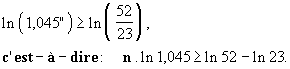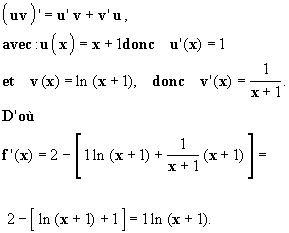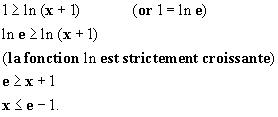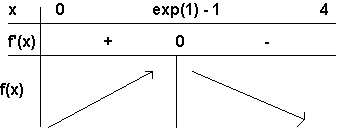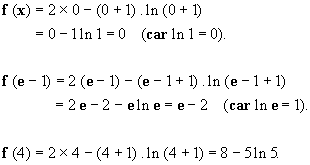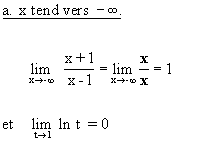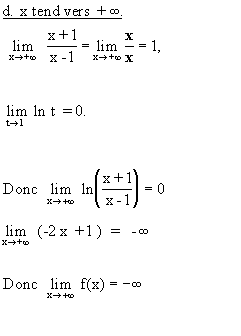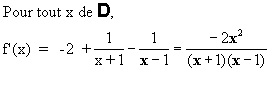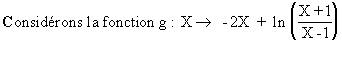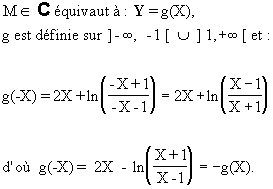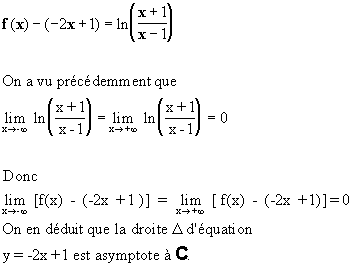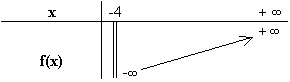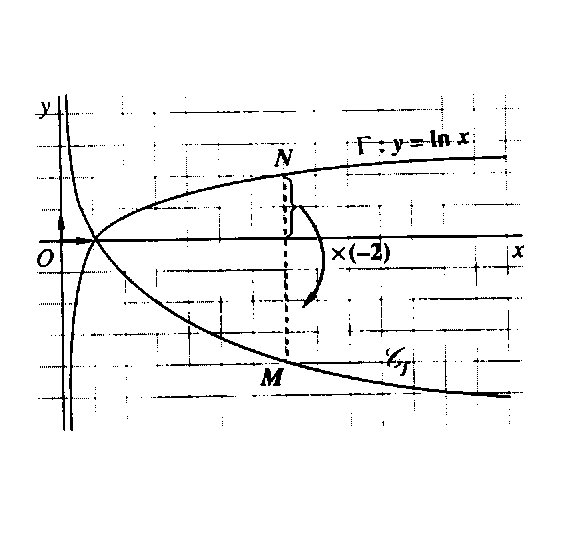|
LOGARITHME
PRÉPARATION INTERROGATION
PRÉPARATION BAC
(12 questions traités en détail)
L
1 ) Résolution d’
équations avec logarithme 3 exercices
EXERCICE 1:
On se propose de résoudre dans 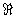 l’équation l’équation 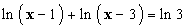 . .
MÉTHODE:
On cherche l’ensemble des x pour
lesquels cette équation existe.
En utilisant les propriétés algébriques de ln, on transforme
l’équation pour se ramener à
: ln (A) = ln(B).
On applique le théorème "la fonction ln est une bijection" :
ln (A) = ln(B) équivaut à A = B,
et on résout l’équation obtenue.
On vérifie si les valeurs trouvées appartiennent à l’ensemble de
définition de l’équation, et on donne l’ensemble solution.
|
SOLUTION : Ensemble de définition :
La quantité dont on prend le logarithme doit être strictement positive.
Pour que l’équation existe, il faut :
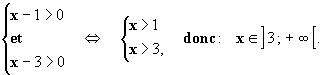
Transformation :
Comme ln a + ln b = ln ab, l’équation devient ln (x
- 1) (x - 3) = ln 3.
Résolution technique:
Comme la fonction ln est une bijection, l’équation équivaut à :

Vérification:
Il faut
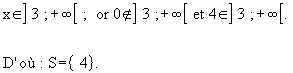
REMARQUES PRATIQUES :
Pour chercher l’ensemble solution, il faut se souvenir qu’il y a
autant d’inéquations à poser que de ln portant sur des expressions différentes
comportant x.
Dans l’écriture de l’équation, si un logarithme est soustrait, il
est préférable de le transposer dans l’autre membre.
Par exemple, l’équation ln x - ln (x + 1) = ln 2 devient ln x = ln
2 + ln (x + 1).
Si tous les ln ne portent que sur x (ou la même expression);
par exemple : 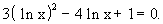
Ne pas confondre
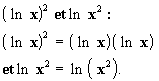
De plus,  existe pour tout réel, sauf 0. existe pour tout réel, sauf 0.
On ne peut résoudre par un procédé algébrique une équation comme 2 x - 1 +
ln (x + 2) = 0, somme d’un polynôme et d’un logarithme de l’inconnue.
Seule une résolution approchée de l’équation f (x) = 0 est possible. |
| Exercice 2 :
Résoudre dans 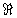 , l’équation : , l’équation :
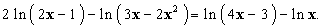
|
Solution :
On cherche l’ensemble de définition de cette équation.
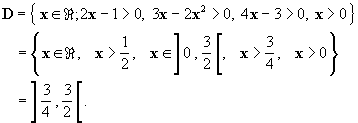
L’équation (E) équivaut à :
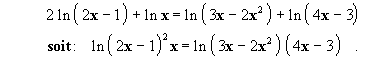
une propriété du cours permet d’obtenir :
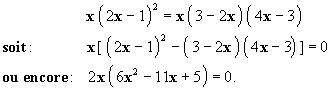
Cette équation équivaut à :

0 n’appartient pas à D. Les solutions de l’équation sont
donc :

MÉTHODE A RETENIR :
- Recherche de l’ensemble de définition D.
- Transformation de l’équation en somme de logarithmes (pour obtenir des
produits plutôt que des quotients).
- Utilisation des théorèmes du cors pour obtenir une égalité entre deux
logarithmes.
- Utilisation de la propriété ln a = ln b donc a = b pour obtenir une
équation sans logarithme.
- Résolution de l’équation - On vérifie que les solutions appartiennent
à D. |
| Exercice 3 : Résoudre
dans R l'équation et l'inéquation suivantes:
2In (x + 1) = In (1 - x) (1)
MÉTHODE :
- Déterminer l'ensemble D de
résolution de l'équation (ou de l' inéquation ).
- Se ramener à l'équation In f(x) = In g(x).
- Ne retenir que les solutions qui appartiennent à D.
|
Solution : L’égalité (1) n'a de
sens que si
x + 1 > 0
et 1 - x > 0, soit - 1 < x < 1.
Ensemble de résolution de l’équation S = ]-1; 1 [.
L ‘équation donnée n’étant pas sous la forme ln f(x) = ln g(x),
elle doit être transformée.
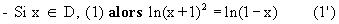


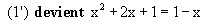
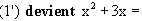

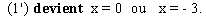
* Parmi les deux nombres trouvés, seul 0 appartient à D;
l'équation (1) admet 0 pour unique solution.
S = { 0 } |
2 ) Résolution d’
inéquations avec logarithme(s) : 4 exercices
EXERCICE 4 :
On se propose de résoudre l’inéquation (un peu compliquée, certes !) :

MÉTHODE
On retrouve les quatre étapes de la méthode de résolution
d’une équation et les mêmes remarques techniques.
Seul le théorème à appliquer change.
On utilise alors : "la fonction ln est strictement croissante
sur 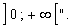
ln A < ln B équivaut à A < b
|
Solution : Ensemble de définition :
La quantité dont on prend le logarithme doit être strictement positive. Pour
que l’inéquation existe, il faut :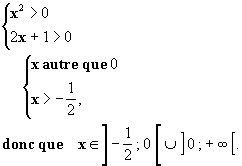
Transformons :
Comme

on peut écrire

Mais ici, x peut être compris entre -
1/2 et 0.
Aussi pour éviter des
erreurs, il est préférable de multiplier chaque membre de l’inéquation par 2.
L’inéquation devient :
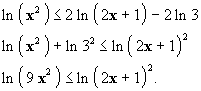
Résolution :
Comme la fonction ln est strictement croissante,
l’inéquation équivaut à :

Vérifions :
Il faut
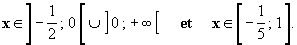
D’où
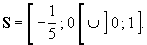
|
EXERCICE 5 :
A. Résoudre dans 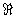 l’inéquation l’inéquation 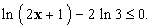
B. Étudier le signe de l’expression
E (x) = ln (1 - x) - 4.
MÉTHODE
A. On retrouve les quatre étapes de la méthode de résolution
d’une équation et les mêmes remarques techniques.
Seul le théorème à appliquer change.
On utilise alors : "la fonction ln est strictement croissante
sur 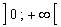 ". ".
 équivaut à équivaut à  . .
Méthode :
B. Pour étudier le signe d’une expression E(x) comportant
ln, on résout l’inéquation 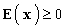 , c’est-à-dire qu’on cherche pour quelles
valeurs de x l’expression est positive ou nulle. , c’est-à-dire qu’on cherche pour quelles
valeurs de x l’expression est positive ou nulle.
Pour toutes les autres valeurs de l’ensemble de définition,
l’expression E(x) sera strictement négative.
|
Solution :
A.
L’inéquation a un sens si : 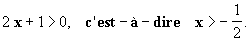
Pour
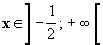 , l’inéquation se transforme en :
, l’inéquation se transforme en :
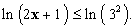
Comme la fonction ln est strictement croissante sur
l’ensemble des réels strictement positifs, l’inéquation s’écrit :

Il faut
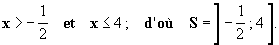
B.
ln (1 - x) - 4 existe lorsque 1 - x > 0, soit x < 1.
On résout
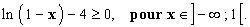
Cette inéquation se transforme en
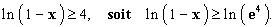
Par la stricte croissance de la fonction ln, l’inéquation équivaut à :

Ainsi, lorsque 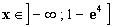 , alors E (x) est positif ou
nul. , alors E (x) est positif ou
nul.
D’où le tableau de signes de E (x) :  |
EXERCICE 6 :
Résoudre dans 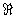 , l’inéquation : , l’inéquation :

|
Solution On cherche l’ensemble de
définition de l’inéquation.

On pose X = Ln 2x.
L’inéquation s’écrit alors :
X3 - 3X² - X < 0
Le polynôme X3 - 3X² - X a pour
racine évidente 1.
il est donc factorisable par (X - 1) :
X3 - 3X² - X = ( X - 1) ( a X²
+ bX + c ) = aX3 + ( b - a ) X² + (c - b )
X - c
Par identification on obtient :
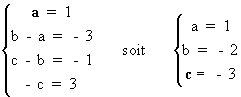
X3 - 3X² - X = ( X - 1) ( X² -
2X - 3 ) = ( X - 1 )( X + 1 ) ( X - 3)

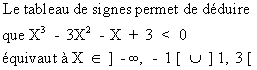
soit: In 2x < - 1 ou 1 < In 2x < 3.
On sait que In e-1 = -1 : ln e =1
; ln e3 = 3.
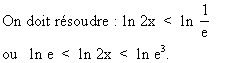
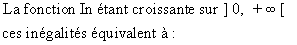


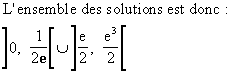
|
| Résoudre : 
MÉTHODE :
- Déterminer l'ensemble D de résolution de l'équation (ou de l' inéquation ).
- Se ramener à l'équation In f(x) = In g(x).
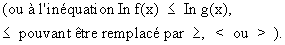

- Ne retenir que les solutions qui appartiennent à D.
|
Solution : L’inégalité
(2) n'a de sens que si
x > 0
et x - 2 > 0
et 2x - 3 > 0, soit x >2.
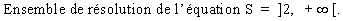
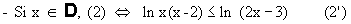
> Mettre l’inéquation donnée sous
la forme ln f(x) < ln g(x).

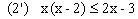
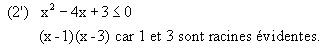

- Les solutions de l'inéquation doivent appartenir à D d’où l'ensemble des solutions est :
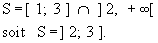
|
3 )
Inéquation où l’inconnue est en exposant
EXERCICE 8 :
Un capital de 23 000 F est placé à 4,5 % à intérêts composés. Sa valeur
acquise au bout de n années est
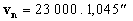
Déterminer à partir de quelle année sa valeur acquise sera supérieure ou
égale à 52 000 F.
MÉTHODE
Pour résoudre une inéquation où l’inconnue est en exposant :
- on utilise la stricte croissance de la fonction ln :
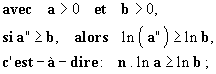 l l
- on divise alors chaque membre de l’inéquation par ln a, en
tenant compte de son signe.
|
SOLUTION : On cherche n, entier
naturel, tel que

On divise chaque membre par 23 000 ; l’inéquation devient :
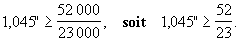
Comme la fonction ln est strictement croissante, on obtient :
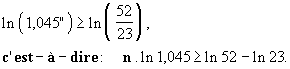
Or 1,045 > 1, donc ln 1,045 > 0 ; on peut ainsi diviser les
deux membres de l’inéquation par ln 1,045 sans changer le sens :

A l’aide de la calculatrice, on obtient :
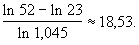
Ainsi, à partir de 19 ans, la valeur acquise de ce capital sera
supérieure à 52 000 F. |
4 ) Étude des variations de fonctions
avec logarithme (2 exercices )
EXERCICE 9 :
On se propose d’étudier les variations de la fonction numérique de la
variable réelle x définie sur l’intervalle
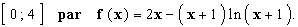
MÉTHODE
- On vérifie que dans l’intervalle donné l’expression f (x) existe,
bien que l’ensemble de définition soit donné ici.
- Comme la fonction ln est dérivable sur son ensemble de définition, on
calcule la dérivée.
- On étudie le signe de l’expression donnant la dérivée.
- On dresse le tableau des variations sur l’ensemble de définition et on
énonce les variations.
|
SOLUTION : La quantité dont on prend le
logarithme doit être strictement positive.
Pour que l’expression f (x) existe, il faut x + 1 > 0
,c’est-à-dire x > - 1. Donc la fonction f est bien définie sur [0 ; 4].
Une fonction logarithme est dérivable sur son ensemble de définition,
donc
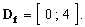
Comme (x +1) ln (x + 1) est un produit, on applique :
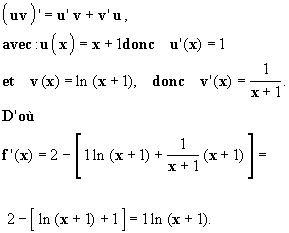
Comme l’expression f ‘(x) comporte encore ln, pour étudier
son signe on résout l’inéquation 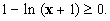
Il faut x > - 1, pour que ln (x + 1) existe.
On transforme l’inéquation :
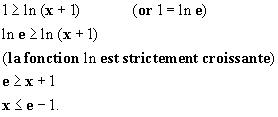
D’où le tableau de signes :

Tableau des variations sur [0 ; 4] :
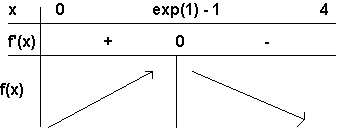
Sur [0 ; e - 1], la dérivée est positive, donc la fonction est
croissante.
Sur [e - 1 ; 4], la dérivée est négative, donc la fonction est
décroissante.
En e - 1, la dérivée s’annule.
On peut, à la suite de cette étude des variations, calculer les
valeurs aux bornes de l’intervalle de définition, ainsi que l’extremum :
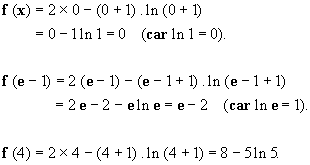
|
Courbe :
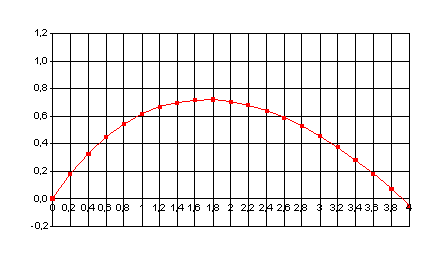
|
| EXERCICE 10 : 1 )
Étudier la fonction f de R dans R définie par :
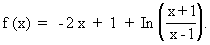
Soit C sa courbe
représentative dans un repère orthogonal (O, i, j) ( unités 2 cm sur l'axe des
abscisses, 1 cm sur l'axe des ordonnées).
2 ) Démontrer que le point I (0, 1) est centre de symétrie de C et que la droite D
d'équation :
y = - 2 x + 1 est asymptote oblique à C.
3 ) Construire C.
MÉTHODES :
1 ) Généralités :


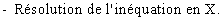
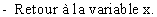

2 ) MÉTHODES A MAÎTRISER :
- Ensemble de définition fondamental (souvent donné dans l'énoncé).
- Bien connaître les théorèmes sur les limites (opérations, composées).
- Pour montrer qu'une fonction logarithmique est impaire, on utilise la
propriété :
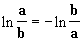
- Pour prouver que la droite A d'équation y = g(x) est asymptote à la courbe
C d'équation y = f(x), il suffit de montrer que :

- Ne pas oublier le tableau de valeurs pour construire la courbe précisément.
On se contente de chercher les coordonnées des points situés sur une des deux
branches.
On complète en utilisant la symétrie par rapport à I.
|
Solution : 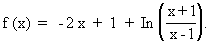
- La fonction f est définie si et seulement si :
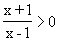
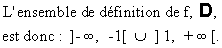
- On étudie les limites de f aux bornes de de D.
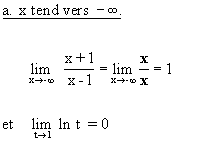
Le théorème sur la limite de fonctions composées permet de
déduire :

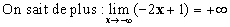
Un théorème sur la limite d'une somme de fonctions permet de
conclure :
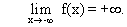


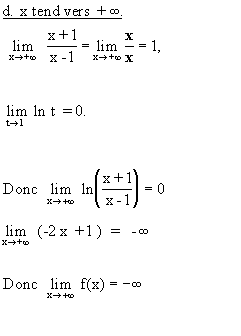
- La fonction f est dérivable sur D
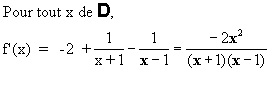
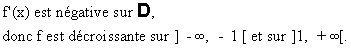
On récapitule tous les résultats dans le tableau de variation ci-dessous.
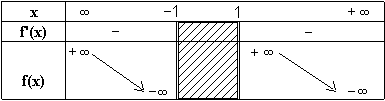
- Pour montrer que I est centre de symétrie de donnons
l'équation de dans le repère ( I , i, j).
M a pour coordonnées (x, y) dans le repère (0, i, j) et (X, Y)
dans le repère (I, i, j).
OM = IM + OI signifie analytiquement: x = X et
y = Y + 1

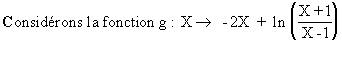
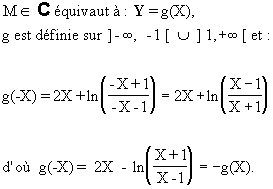
g est impaire. Donc C
est symétrique par rapport à I.
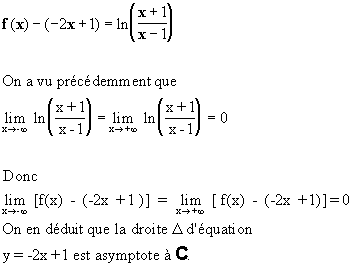
- Tableau de valeurs :
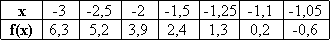
|
Exercice 11 :
| Étudier et représenter la fonction f définie sur ]- 4 ;
+00 [ par : f (x) = ln(x + 4) + 3.
Méthode :
Si la fonction f est telle que f (x) = In (x - a) + b, alors la courbe de la fonction f est la transformée de la courbe
F d'équation y = In x
dans la translation de vecteur V(a; b).
La fonction f a même sens de variation que In.
|
Solution : Comme f (x) = In (x + 4) + 3
est de la forme In
(x - a) + b,
avec a = - 4 et b = 3,
la courbe F d'équation y = ln x se transforme en Cf
dans la translation de vecteur V(- 4; 3).
D'où le tableau complet des variations :
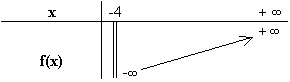
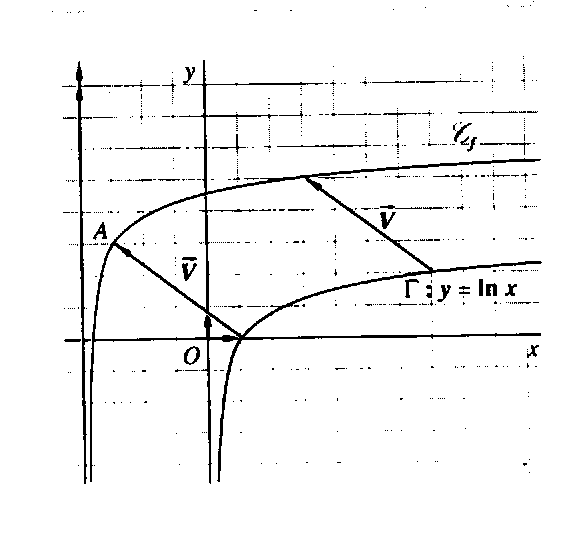
Le point A (- 3 ; 3) est un point de Cf
la droite d'équation x =- 4 est asymptote verticale à la courbe Cf. |
Exercice 12 :
| Étudier et représenter la fonction f définie sur
]- 4 ; +00 [ par : f(x) = - 2 . Lnx
MÉTHODES :
Si la fonction f est telle que f (x) = k . In x, alors en multipliant par k
l'ordonnée de chaque point N( x ; ln x) de z d' d'équation y
= In x, on obtient les points M(x; k.ln x) de la courbe Cf
.
|
Solution : 
D'où le tableau complet des variations :

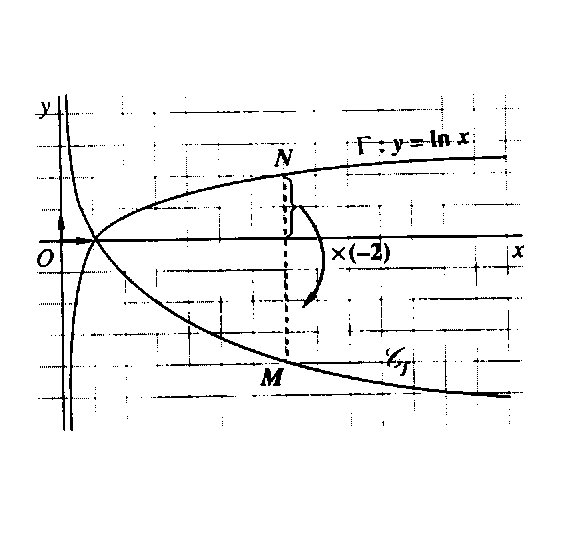
|
|

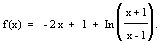
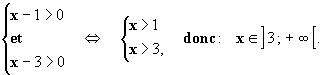

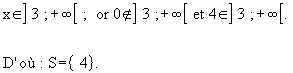
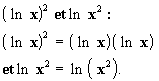
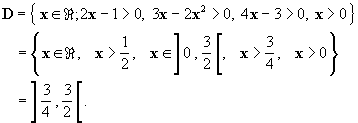
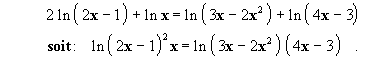
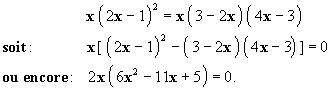

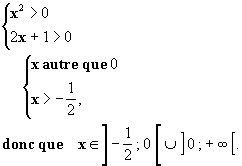


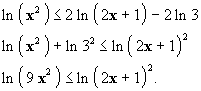

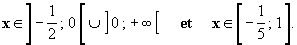
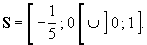
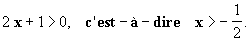
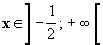 , l’inéquation se transforme en :
, l’inéquation se transforme en :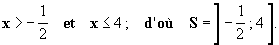

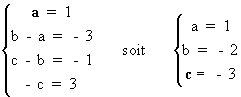

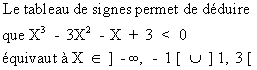
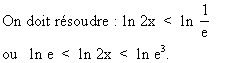
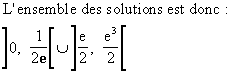
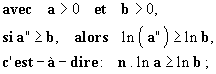 l
l