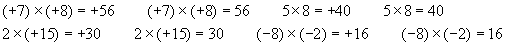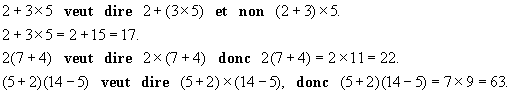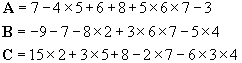CALCULS AVEC DES NOMBRES RELATIFS

CH 1 CALCULS NUMÉRIQUES

CALCULS AVEC DES NOMBRES RELATIFS
26 exercices corrigés en détail

PRÉPARATION INTERROGATION : 26 exercices corrigés en détail

L’ESSENTIEL DU COURS A MAÎTRISER PARFAITEMENT:

                                    Addition :                                 Opposé d'un nombre :

                                        Multiplication : Règle des signes

                                        Multiplication et addition : priorité

MÉTHODES DE CALCULS:

Effectuer un calcul avec des additions et des multiplications.
Méthode ,exemple

Effectuer un calcul avec des parenthèses. Méthode 1 exemple traité

Effectuer un calcul avec des parenthèses et des crochets précédés
de signes + ou -. ( 1 exemple en chiffres , 1 exemple en lettres)

Multiplication et calcul littéral Méthode , 1 exemple traité

Effectuer un calcul littéral avec des additions et des multiplications

Effectuer un calcul du type a(b+c) : Méthode , 1 exemple , 1exemple traité

Effectuer un calcul du type (a+b)(c+d) : Méthode 1 exemple traité

I - L’ESSENTIEL DU COURS :

1) ADDITION

Règles d’utilisation:

Pour tous les nombres a, b, c:

a + b = b + a

( a + b ) + c = a + ( b + c )

a + 0 = 0 + a = a

Exemples:

Pour a = 7 , b = - 8 , c = 4 ;

7 + ( - 8) = - 1 ( - 8 ) + 7 = - 1

( 7 + ( - 8 ) )+ 4 = ( - 1 ) + 4 = 3

7 + ( ( - 8 ) + 4 ) = 7 + ( - 4 ) = 3

7 + 0 = 0 + 7 = 7

Opposé d' un nombre :

Pour tout nombre a il existe un nombre noté - a, appelé opposé de a tel que:
a + ( - a ) = 0 et ( - a ) + a = 0

- a veut seulement dire "opposé de a".

Ne pas confondre avec nombre négatif.

l’opposé d’une somme est la somme des opposés:

- ( a + b ) =( - a ) + ( - b )

2 ) MULTIPLICATIONS

Règles des signes :

A/ Le produit de deux nombres de même signe est un nombre positif, c’est à dire un nombre plus grand que 0, qui s’écrit avec un signe + ou sans signe.
Exemples:

B/ Le produit de deux nombres de signes différents est un nombre négatif, c’est à dire un nombre plus petit que 0, qui s’écrit avec un signe - .

Exemples:

Multiplications et additions.

La multiplication a priorité sur l’addition.

3 Exemples :

II - MÉTHODES

Effectuer un calcul avec des additions et des multiplications.

MÉTHODE :
          1/ Effectuer les multiplications                                             2/ Effectuer les additions

Exemple:

Solution:

Il faut d’abord effectuer les multiplications:

A = 3 - ( - 10 ) - 10 - 30 +7 - 4 + ( - 45 )

Puis, effectuer les additions (en utilisant les règles du chapitre 1)

A = 3 + 10 - 10 - 30 + 7 - 4 - 45

A = - 69

Effectuer un calcul avec des parenthèses.

MÉTHODE
Il faut d’abord effectuer les calculs dans les parenthèses.

EXEMPLE :
calculer :

A = 110 + 2(5 - 4x6)(7x4 - 8) - 3 + 5x6 - ( 19 - 7 x6)

Solution:
A = 110 + 2(5 - 4 x 6)(7x4 - 8 ) - 3 + 5x6 - (19 -7x6)
A = 1 1 0 + 2 ( 5 - 24 ) ( 28 - 8 ) - 3 + 30 - ( 19 - 42 )

A = 110 + 2 ( - 19 ) ( 20 ) - 3 + 30 - ( - 23 )

A = 110 - 760 - 3 + 30 + 23

A = - 600.

Effectuer un calcul avec des parenthèses et des crochets précédés de signes + ou -.

MÉTHODE :
Dans une écriture avec des parenthèses et crochets, on supprime d’abord les parenthèses enfermées dans les crochets avant de supprimer les crochets.

Il faut d’abord calculer le nombre que représente chaque parenthèse, puis faire de même avec chaque crochet.

EXEMPLE I :( avec des lettres)
Sachant que :
a = 3 , b = 5 , c = - 4 , d =8 et e = - 10 ;

calculer:

C =
3 - [ 7+ ( a - b ) ] + 9 - ( - 4 + c ) + [ 4 - ( - d + e )]

SOLUTION :
Supprimons les parenthèses:

C= 3 - [ 7 + ( a - b ) ] + 9 - ( - 4 + c ) + [4 - ( - d + e )]

C = 3 - [ 7 + a - b ] + 9 + 4 - c + [ 4 + d - e ]

Supprimons les crochets:

C = 3 - [ 7 + a - b ] + 9 + 4 - c + [ 4 +d - e ]

C = 3 - 7 - a + b + 9 + 4 - c + 4 + d - e

remplaçons a, b, c, d, e par leurs valeurs         respectives:

C=
3 - 7 - ( 3 ) + ( 5 ) + 9 + 4 - ( - 4 ) + 4 + ( 8 ) - ( - 10 )

C = 3 - 7 - 3 + 5 + 9 + 4 + 4 + 4 + 8 + 10

C = 37

Exemple II: ( avec des chiffres)

Calculer :

13 - 3x7 - 2[ 7 - 4(8 - 3x2) + 5 - ( 7 - 4x6)

Solution:

A = 13 - 21 - 2 [ 7 - 4 ( 8 - 6 ) ] + 5 - ( 7 - 24 )

A = 13 - 21 - 2 [ 7 - 8 ] + 5 + 17

A = 13 - 21 - 2 ( - 1 ) + 5 + 17

A = 13 - 21 + 2 + 5 + 17

A = 16

Multiplication et calcul littéral :

Pour tout nombre a, b, c:

Effectuer un calcul littéral avec des additions et des multiplications

Exemple:
Calculer:

A =
3a - 7a x 2b + 8 - 4b x 5a
+ 7a - 9 + 4b

Solution:
Il faut d’abord effectuer les multiplications:

A = 3a - 14ab + 8 - 21ba + 7a - 9 + ab

puis effectuer les additions, on remarquant que:

A = 10a - 34 ab + 4b - 1

Pour vérifier ce résultat, il est possible de donner des valeurs simples pour a et b puis de calculer A en utilisant d’une part l’énoncé et d’autre part le résultat.

Prenons a = 1 et b = 3 .

En utilisant l’énoncé:

A = 3 - 42 + 8 - 60 + 7 - 9 + 12

A = - 81

En utilisant ce résultat:

A = 10 - 102 + 12 - 1

A = - 81

Les deux résultats doivent, bien sûr, être les mêmes.

Effectuer un calcul du type a(b+c) :

MÉTHODE :

On utilise les règles précédentes et la règle:

Exemple :

Calculer A

A = 2 + 5( 2a + 3 ) + 4
     + (3 - 4a ) - 3( 4 - 3a )

Solution:
On effectue d’abord les multiplications repérées:

D’où: A = 2 + 10a + 15 + 4 + 3 - 4a - 12 + 9a

A = 15 a + 12

Effectuer un calcul du type (a+b)(c+d) :

MÉTHODE :
On utilise toujours les règles précédentes et la règle:

EXEMPLE :

Calculer A

A=
2 + ( 3 - a) ( 2b + 4 )- 4 -3 ( 2 -3 b )( 4 - a )

Solution:
On applique d’abord la règle :
( a + b ) ( c + d )= a c + a d + b c + b d
sur les multiplications repérées:

( 3 - a ) ( 2 b + 4 ) = 6b + 12 - 2 ab - 4a

( 2 - 3b ) ( 4 - a ) = 8 - 2a - 12b + 3ab

Puis on utilise les règles:

A =
2 + (6b + 12 - 2ab - 4a ) - 4 - 3 ( 8 - 2a - 12b + 3ab )

A = 2 + 6b + 12 - 2ab - 4a - 4 -24 + 6a + 36b - 9ab

A = 2a + 42b - 11ab -14

Développer un calcul, c’est faire disparaître toutes les parenthèses (et les crochets).

Réduire un calcul, c’est l’écrire sous la forme la plus courte possible.

III - PRÉPARATION INTERROGATION : 26 exercices corrigés

EXERCICE 1:
sachant que :
a = 3 , b = - 5 , c = - 4 , et d = 8 ;

calculer: A = 7- a + b - c + d

Solution 1:

Il faut remplacer a,b,c et d par leur valeurs respectives:

A = 7 - ( 3 ) + (- 5 ) - ( - 4 ) + ( 8 )

A = 7 - 3 - 5 + 4 + 8

A = 11 ( Remarquer que - 3 - 5 + 8 = 0 )

EXERCICE 2 :
sachant que :
a = 4 , b = - 6 , c = 2 e t d = - 7 ;

calculer : B

B = - 8 - ( - 5 + a ) + b + ( - 3 + c ) + ( 9 - d )

Solution 2:
Supprimer d’abord les parenthèses:

B = - 8 + 5 - a + b - 3 + c+ 9 - d

Remplacer a, b, c, et d par leurs valeurs respectives:

B = - 8 + 5 - ( 4 ) + ( - 6 ) - 3 + ( 2 ) + 9 - ( - 7 )

B = - 8 + 5 - 4 - 6 - 3 + 2 + 9 + 7

B = 2

EXERCICE 3 :
Sachant que
a = - 4 , b = - 17 , c =15 , d = 23 , e = - 11 ,
f = 13 ,
calculer:

A = 4 - a + b - c

Solution 3:

A = 4 - ( - 4 ) + ( - 17 ) - ( 15 )

A = 4 + 4 - 17 - 15

A = - 24

EXERCICE 4 :
sachant que
a = 11,3 , b = - 7 , c = 0,23 , et d = 25

calculer:

A = 3,7 - a - ( 7 - b ) + ( - c + d ) - 4

Solution 4:

A = 3,7 - a - 7 + b - c + d - 4

A = 3,7 - 11,3 - 7 - 7 - 0,23 + 2 5 - 4

A = - 0,83

EXERCICE 5 :

sachant que
a = 11,3 , b = - 7 , c = 0,23 , et d = 25

calculer:

B = 8 - (- a + 4,2 ) - b +( 7 - c - a )

Solution 5:
B = 8 + a - 4,2 - b + 7 - c - a

B = 8 + 11,3 - 4,2 + 7,12 + 7 - 0,23 - 11,3

B = 17,69

EXERCICE 6 :
sachant que
a = 11,3 , b = - 7 , c = 0,23 , et d = 25

calculer:

C = - d + 3,2 + a - ( - b + c ) + ( - 3,2 + b )

Solution 6:

C = - d + 3,2 + a + b - c - 3,2 + b

C = - 25 + 3,2 + 11,3 - 7,12 - 0,23 -3,2 - 7,12

C = - 28,17

EXERCICE 7 :
sachant que
a = 3 , b = 5 , c = - 4 , et e = - 10

calculer:

D = 8 + [ - 9 - ( a - 3 - c ) ] - ( b - 4 ) [ 7 + ( 2 - e) ]

Solution 7:

D = 8 + [ - 9 - a + 3 + c ] - b + 4 - [ 7 + 2 - e ]

D = 8 - 9 - a + 3 + c - b + 4 - 7 - 2 + e

D = 8 - 9 - 3 + 3 - 4 - 5 + 4 - 7 - 2 - 10

D = - 25

EXERCICE 8 :

Sachant que
a = 7 , b =- 11 , c= - 12 , d = 17 , e = 21
et f = - 25 ;

calculer:

A = 7 - ( 5 - a ) - [ 7 - ( b - 3 ) ]

Solution 8 :
A = 7 - 5 + a - [ 7 - b + 3 ]

A = 7 - 5 + a - 7 + b - 3

A = 7 - 5 + 7 - 7 - 1 1 - 3

A = - 12

EXERCICE 9 :

Sachant que
a = 7 , b =- 11 , c= - 12 , d = 17 ,
e = 21 et f = - 25 ;

calculer:

B = - 9 + ( - b + 4 ) + [ - 7 - ( - c + a - 3 ) ]

Solution 9 :
B = - 9 - b + 4 + [ - 7 + c - a + 3 ]

B = - 9 - b + 4 - 7 + c - a + 3

B = - 9 + 11 + 4 - 7 - 12 - 7 + 3

B = - 17

EXERCICE 10 :

Sachant que
a = 7 , b =- 11 , c= - 12 , d = 17 ,
e = 21 et f = - 25 ;

calculer:

C = a - [ 7 - ( 3 - c ) + ( b - 2 ) ] + [ - 5 - ( a - d ) ]
Solution 10 :
C = a - [ 7 - 3 + c + b - 2 ] + [ - 5 - a + d ]

C= a - 7 + 3 - c - b + 2 - 5 - a + d

C = 33

EXERCICE 11 :

Sachant que
a = 2 , 03 ; b = - 0,7 ; c = - 11,4 ; d = 23,57

calculer:

D = - a - ( 8,2 - b ) + [- c - ( a - d + b ) ]

Solution 11 :

D = - a - 8,2 + b + [ -c - a + d- b ]

D = - a - 8,2 + b -c - a + d- b

D = - 2,03 - 8,2 - 0,7 + 11,4 - 2,03 + 23,57 + 0,7

D = 22,71

EXERCICE n°12       n°13       n° 14

Calculer:

Solution n°11 n° 12 n° 13

A = 7 - 20 + 6 + 8 + 210 - 3
A = 208

B = - 9 - 7 -16 + 126 - 20
B = 74

C = 30 + 15 +8 - 14 - 72
C = - 33

EXERCICES n° 14 :

Calculer :

A =
25 - 4(7 - 2x9 + 15 ) - 12 + 6x5 + 3 - (9x8 - 6)

Solution :n° 14 ;n° 15 :

A =
25 - 4 ( 7 - 18 + 15 ) - 12 + 30 + 3 - (72 - 6 )

A = 25 - 4 ( 4 ) -12 + 30 + 3 - 66

A = 25 - 16 - 12 + 30 + 3 - 66

A = - 36

EXERCICES n° 15 :
B =
- 12 x 3 + 7 + 2 (5x3 - 6) - 5 + ( 4 - 3x6 )(7x2 - 5 + 4x3)

Solution n°15

B = - 36 + 7 + 2 ( 15 - 6 ) - 5 + ( 4 - 18 ) ( 14 - 5 + 12 )

B = - 36 + 7 + 18 - 5 - 294

EXERCICE 16 :
Calculer:

A =
12 + 6 ( 8 - 4 x 5 ) - 19 +3 [ 9 - ( 5 x 7 - 17 ) ]

Solution 16:

A = 12 + 6 ( 8 - 20 ) - 19 + 3 [ 9 - ( 35 - 17 ) ]

A = 12 + 6 ( - 12 ) - 19 + 3 [ 9 - 18 ]

A = 12 - 72 - 19 + 3 ( - 9 )

A = - 106

EXERCICE 17 :

Calculer:

B =
4 x 2 - 12 - ( 17 - 3 x 12 ) - [ 5 - ( 4 - 7 x 2)(3 x 8 - 6 )]

Solution 17:

B = 8 - 12 - ( 17 -36 ) - [ 5 - ( 4 - 14 ) ( 24 - 6 ) ]

B = 8 - 12 - ( - 19 ) - [ 5 - ( - 10 ) (18 ) ]

B = 8 - 12 + 19 - [ 5 + 180 ]

B = 8 -12 + 19 - 185

B = - 170

EXERCICE 18 et 19 :

Sachant que a = - 2 , b = 7 , c = - 5 .

calculer :

Solution 18 et 19 :

A = - 6 - 28 + 140 + 40

A = 146

B = - 30 - 2 + 14 - 1680 + 60

B= - 1638

EXERCICE 20 , 21, 22, 23

Simplifier l’écriture des expressions suivantes puis vérifier le résultat avec
a = - 1 , b = 2 , c = - 2 .

Solution A :

A = 3 - 5 a + 6ab - 5b - 4a -6ab + 9

A = 12 - 9a - 5b

Vérification:

A =
3 - 5 (-1) + 2(2) x 3(-1) - 5(2) - 4(-1) -2(-1) x 3(2) + 9
A = 3 + 5 -12 - 10 + 4 + 12 + 9

A = 11

Solution B :

B = 7ac - 3ab + 4b - 10ac + 2ab + 3ac + ab

B = 4b

Vérification:

B = 14 + 6 + 8 - 20 - 4 + 6 - 2

Solution C :

C =
4b + 2a - 12 a -15b + 4 - 6ab + 11b + 10a

C = 4 - 6ab

Vérification:

C = 8 - 2 + 12 - 30 + 4 + 12 + 22 - 10 = 16

C = 4 + 12 = 16

Solution D :

D = 2ac + 6ab - abc

Vérification

D = - 12

EXERCICE 24 :

Développer, réduire puis vérifier le résultat avec a = -1 et b = 2.

A = 5 - 3 (2a + b ) - 5 + 4 ( 2a - 5b )

Solution A :

A = 5 - 6a - 3b - 5 + 8a - 20 b A = 2a - 23b

Vérification:

A = 5 - 3 ( - 2 + 2 ) - 5 + 4 ( - 2 - 10 )

A = 5 - 5 - 48

A = - 48

EXERCICE 25 :

Développer, réduire puis vérifier le résultat avec a = -1 et b = 2.

B =
7b + 4 - ( 8a - 2b + 3 ) - 4 + 2 (4a - 5b + 8 )

solution B :

B = 7b + 4 - 8a + 2b - 3 - 4 + 8a - 10b + 16

B = 13 - b

Vérification:

B = 11

EXERCICE 26 :

Développer, réduire puis vérifier le résultat avec a = -1 et b = 2.

C = 4 - 4a ( 5 - 3b ) - 2 + 6b ( 3 -2a )

solution C :

C = 4 - 20 a + 1 2ab - 2 + 18 b-12ab

C = 2 -20a +18b

Vérification:

C= 58